| GCD |
[Features] To find solution of
greatest common divisor.
[Format] GCD(n1,n2)
[e.g.]
print gcd(30,42)
6
| LCM |
[Features] To find solution of least
common multiple.
[Format] LCM(n1,n2)
[e.g.]
print lcm(30,42)
210
| PRIME |
[Features] To return the first prime
number on and after a specified number.
[Format] PRIME(n)
[Explanation]
When n is a prime number, n is
returned,
so it can also use
for distinction of whether n is prime number.
[e.g.]
print prime(12)
13
| ROOT |
[Features] To find the n-th root of
x.
[Format] ROOT(n,x)
[Explanation]
This is an approximation.
n√x (n is dimensions number, the
upper left mini symbol, not multiplication)
A number that is multiplied by 'n'
times to became 'x'.
SQR is
only the square, it can find n-th root of three or more dimensions.
[e.g.]
r=root(3,100)
print r
4.6415889136718755
print r^3
100.00000517446294
| FAC |
[Features] The factorial of n is
returned.
[Format] FAC(n)
[Explanation]
(The product of all the integers
from 1 to n)
The case of
'fac(5)', it will be 1*2*3*4*5=120.
[e.g.]
print fac(5)
120
| PERM |
[Features] To return number of cases
of permutation of mathematics.
[Format] PERM(n,r)
[Explanation]
It is calculation represented by
'nPr'.
The total number of
branches that take 'r' pieces out
from different 'n' pieces,
and put in order.
The case of
'6P3', it will be 6*5*4=120.
[e.g.]
print perm(6,3)
120
| COMB |
[Features] To return number of cases
of combination of mathematics.
[Format] COMB(n,r)
[Explanation]
It is calculation represented by
'nCr'.
The total pattern number
that select 'r' pieces from different 'n' pieces.
This value is obtained by
PERM(n,r)/FAC(r).
[e.g.]
print comb(5,3)
10
| SIGMA |
[Features] The sum of number
sequence is calculated.(mathematics Σ)
[Format] SIGMA(n1,n2)
[Explanation]
4
Σ (x+1) (in this casen1=1,n2=4)
x=1
The case 'sigma("x+1",1,4)'
then,
to substitute '1 to
4: increasing' for 'formula x',
and the value adding all the
results is returned.
This
'formula of Σ' can be calculated including general functions as
sin(),cos(),etc.
It also have the function to make
various settings.
Form2:
sigma("int"|"even"|"odd")
Although increment is usually 1,(default a=sigma("int"))
it can specify the following.
add only when even:
a=sigma("even")
add only when
odd : a=sigma("odd")
And although the target
variable is 'x' by default,
it can change into any
variables by 'a=sigma("v:y")'.
Form2: sigma("v:1chaVariableName")
(to describe 1character
Variable-Name next to "v:)
The
variable specified here is also applied to target variable of
differential/Integration/fcal function.
[e.g.]
print sigma("2*x^2+1",1,4)
64
a=sigma("v:y")
print sigma("2*y^2+1",1,4)
64
a=sigma("odd"):a=sigma("v:x")
print sigma("2*x^2+1",1,4)
22
| DERIV$ |
[Features] The given formula is
differentiated and it is made a Derivative function.
[Format] DERIV$(formula-string)
[Explanation]
The result is returned
by the formula of a character string.
f'(x)=lim f(x+h)-f(x)
h→0 /h
formula "x^n" then, Derivative
function of result will be "n*x^(n-1)"
[e.g.]
print deriv$("x^2+2*x+1")
2*x+2
| DIFF |
[Features] To find solution of
Differential coefficient.
[Format] DIFF(formula-string,n)
[Explanation]
The formula is made into
Derivative function,
and
the value which substituted 'n' for 'x' is acquired.
Differential coefficient will be
the slope of a tangent at the time of the formula'x=n'.
[e.g.]
print diff("x^2+2*x+1",4)
10
| INTGR$ |
[Features] The given formula is
integrated and it is made a Primitive function.
[Format] INTGR$(formula-string)
[Explanation]
∫ f(x)
dx [f(x) is "2*x+2" in example case]
It is returned by the formula of a
character string.
Integration
is the inverse operation of differentiation.
formula "a*x^n" then, the result
formula of integration will be "a/(n+1)*x^(n+1)"
The result is the one without the
integral constant 'C'.
[e.g.]
print intgr$("2*x+2")
x^2+2*x
print intgr$("x^2+5*x")
(1/3)*x^3+(5/2)*x^2
| DINT |
[Features] To find solution of
Definite integral.
[Format] DINT(formula-string,n1,n2)
[Explanation]
4
∫ f(x)
dx [f(x) is "2*x+2" in example case]
1
The formula is made into Primitive
function F(x),
and
substitute 'x' for 'n1' and 'n2',
and the value F(n2)-F(n1) is
acquired.
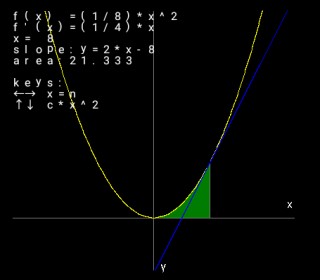
When formula is
'x^2', Definite integral result become an area of part
enclosed between x-axis
and parabola of formula, rangen1<=x<=n2.
[e.g.]
print dint("2*x+2",1,4)
21
| FCAL |
[Features] To calculate formula 1
and 2 for 'x'(default) given by string, and return the result as string.
[Format] FCAL(formula-string1,formula-string2,"add"|"sub"|"mult")
[Explanation]
To specify "add" or
"sub"(subtraction) or "mult"(multiplication) with 3rd parameter.
It is possible to calculate
formula whose coefficient is integer.
The formula including fractions
are not supported at the moment.
[e.g.]
print fcal("x+3","2*x+2","add")
3*x+5
print
fcal("x^2+1","2x-2","mult")
2*x^3-2*x^2+2*x-2
In this page, to deal with the
mathematics function of school textbook.
Mainly, Differential, Integral and
Calculation of sum Σ.
Practical usage is described at
lower part of the reference.
The formula about 'x' are dealt
with by character string.
So
formula level operations in string are possible.
About omission of "*"
3x^2+4x+1…(1)
3*x^2+4*x+1…(2)
In mathematics, it is usually
written like -(1).
The formula
recognized by 'Basic' need '*'(multiplication)
in front of the variable'x'
without omission like -(2).
The formula to give to
function, it is possible to use both (1) and (2).
((1) is converted to (2)
internally, and processed)
The
formula(string) returned by function is always returned in format-(2).
The formula(string) returned by
format-(2),
it is, -by
assigning a numerical value for 'x',
it can calculate by 'calc()' as it
is, and able to get the value.
e.g.
f$=fcal("x+3","2*x+2","add")
:'2-formulas are added and result'3*x+5' enter to 'f$'
x=2 :'substitute 2 for x
print calc(f$) :'calculate '3*x+5'
with assigned value
11
:'result'11' is displayed
And, 'x'-coefficient of formula's
calculation result,
it may
become irrational number which cannot divide,
then, the result output of formula
will be returned by not [a decimal]
but [fraction enclosed by
parentheses], like a "(1/3)*x^3+(5/2)*x^2".
e.g. in the case of integral
calculation
print
intgr$("x^2+5*x")
(1/3)*x^3+(5/2)*x^2