学校テキストでの数学関数

　数学関数実践編
　式の計算、Σの計算、微分・積分

　*微分・積分についてはサンプルプログラム "smp_diff.bas" がありますのでそちらも参照下さい。
   

　式の計算
　xについての式の演算
　x+4 と 2x+1 を加算して 3x+5 の式を得るといった処理が
　当プログラミング言語で可能となりました。

　実際にやってみましょう。
　f$=fcal("x+4","2x+1","add")
　print f$
　3*x+5

　文字列で式を渡して返し値も文字列で返ってきます。
　ここでは足し算"add"を使いましたが他にも引き算"sub"、掛け算"mult"が使えます。

　ここで得られた式は実際に計算させることができます。
　まず xに代入したい値を入れます。
　x=4
　次にcalc()関数を使って式を計算させます。
　print calc("3*x+5")
　 17
　x=4での式の計算値（数値）を得ることができました。

　■ Σを使った数列の和の計算
　　4
　　Σ(2x+1)
　　x=1
　xに1から4までの値を代入していき、その結果を全て加算した値を求めます。
　Basicの関数で記述すると次のようになります。
　print sigma("2x+1",1,4)
　 24
　Σでの和の計算値 24が得られました。
　このΣの式ではsin(),cos()等、Basicの一般関数を式中に含めて計算させることができます。

　■ 微分・積分
　x^2の微分係数は放物線の接線の傾きです。
　　f'(x)=lim  f(x+h)-f(x)
　　      h→0      /h

　x^nを微分した導関数はこのようになります。
　n*x^(n-1)

　実際にBasicの関数を使って式を微分してみましょう。
　式　x^2+2*x+1　を微分します。
　f$=deriv$("x^2+2*x+1")
　print f$
　2*x+2
　導関数の式が得られました。

　■ 微分係数
　今度は実際に xに値を入れて微分係数を求めてみましょう。
　print diff("x^2+2*x+1",4)
　 10
　微分係数 10が得られました。
　これが x=4 の時の接線の傾きになります。

　■ 積分
　微分の逆演算を行うのが積分です。
　先程の導関数を積分してみます。
　print intgr$("2*x+2")
　x^2+2*x
　積分定数Cを除いた原始関数が得られました。

　■ 定積分
　次はxの区間を指定した定積分を求めてみましょう。
　　b
　∫ f(x) dx
　　a
　数学での記述です。
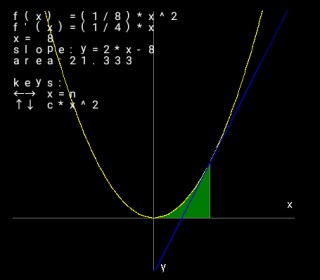
　x^2の式で定積分は指定区間とx軸と式の放物線の間で囲われた部分の面積となります。

　このBasicの関数でa=1,b=4 f(x)=x^2+3 の定積分を求めるにはこのように書きます。
　s=dint("x^2+3",1,4)
　print s
　 29.999999999999996
　定積分の値が得られました。

　微分・積分、Σについての説明はここまでですが
　他にも累乗根、素数、順列、組み合わせ、最大公約数、最小公倍数
　等のの関数が使えます。
　以下、各数学関数のリファレンスマニュアルになります。
　式記述での　3*x→3x　のように *（掛ける）を省略した記述については一番下部のところで解説しています。

GCD

　［機能］　2つの数の最大公約数を求めます。

　［書式］　GCD(n1,n2)

　［例］
     print gcd(30,42)
      6


 

LCM

　［機能］　2つの数の最小公倍数を求めます。

　［書式］　LCM(n1,n2)

　［例］
     print lcm(30,42)
      210


 

PRIME

　［機能］　指定した数値以降での最初の素数を返します。

　［書式］　PRIME(n)

　［説明］
　　nで指定した数以降で最初にくる素数を返します。
　　nが素数の時はnを返すのでnが素数であるかどうかの判別にも使えます。

　［例］
     print prime(12)
      13


 

ROOT

　［機能］　累乗根の近似値を求めます。

　［書式］　ROOT(次元の数n, s)

　［説明］
　　n√s　の値を返します。（nは掛け算でない左上の小文字）
　　n乗してsになる数値です。
　　SQRは2次元の平方のみですがこれは3次元以上の累乗根を求める事ができます。
　　値は近似値となります。

　［例］
     r=root(3,100)
     print r
      4.6415889136718755
     print r^3
      100.00000517446294


 

FAC

　［機能］　n の階乗（1からnまでのすべての整数の積）を得ます。

　［書式］　FAC(n)

　［説明］
　　fac(5)の場合は 1*2*3*4*5=120 となります。

　［例］
     print fac(5)
      120


 

PERM

　［機能］　順列(permutation)での場合の数を求めます。

　［書式］　PERM(n,r)

　［説明］
　　数学で nPr で表される計算です。
　　異なる n個のものから r個を取り出して 1列に並べていった樹形図の枝の総数です。
　　6P3 ならば 6*5*4=120 になります。

　［例］
     print perm(6,3)
      120


 

COMB

　［機能］　組み合わせ(combination)での場合の数を求めます。

　［書式］　COMB(n,r)

　［説明］
　　数学で nCr で表される計算です。
　　異なる n個のものから r個を選ぶパターンの数です。
　　この値は PERM(n,r)/FAC(r) で得られます。


　［例］
     print comb(5,3)
      10


 

SIGMA

　［機能］　数列の和（Σ）を求めます。

　［書式］　SIGMA(式の文字列,n1,n2)

　［説明］
　　4
　　Σ(x+1)　　数学のΣの和の計算を行います。（この場合はn1=1,n2=4）
　　x=1
　　sigma("x+1",1,4)ならば式の xに1から順に増加させて4までを
　　代入させていき、その結果を全て加算した値を返します。
　　このΣの式ではsin(),cos()等、Basicの一般関数を式中に含めて計算させることができます。

　　各種設定をする機能も持っています。
　　書式2：sigma("int"|"even"|"odd")
　　n1,n2への増分は通常1（デフォルトa=sigma("int")）ですが
　　偶数時だけ加算a=sigma("even")、奇数だけ加算a=sigma("odd")
　　の指定ができます。

　　またデフォルトで対象の変数はxですが、a=sigma("v:y")で任意の変数に変更できます。
　　書式3：sigma("v:1文字変数名")
　　（v:の後ろに使用する1文字変数を記述します）
　　ここで指定した変数は微分積分関数での対象変数やFCAL関数の変数にも適用されます。

　［例］
     print sigma("2*x^2+1",1,4)
      64
     a=sigma("v:y")
     print sigma("2*y^2+1",1,4)
      64
    a=sigma("odd"):a=sigma("v:x")
     print sigma("2*x^2+1",1,4)
      22


 

DERIV$

　［機能］　与えられた式を微分して導関数の式を文字列で返します。

　［書式］　DERIV$(式の文字列)

　［説明］
　　導関数
　　　f'(x)=lim  f(x+h)-f(x)
　　　       h→0      /h
　　式が x^n ならば導関数は n*x^(n-1) が結果の式となります。

　［例］
     print deriv$("x^2+2*x+1")
      2*x+2


 

DIFF

　［機能］　微分係数（数値）を求めます。

　［書式］　DIFF(式の文字列,n)

　［説明］
　　式を導関数にしてxにnを代入した値が得られます。
　　微分係数はその式のx=nの時点での接線の傾きになります。

　［例］
     print diff("x^2+2*x+1",4)
      10


 

INTGR$

　［機能］　与えられた式を積分して結果の式を文字列で返します。

　［書式］　INTGR$(式の文字列)

　［説明］
　　∫ f(x) dx　　（f(x)は式の文字列で例の場合だと 2*x+2）
　　積分の式は a*x^n ならば a/(n+1)*x^(n+1) が結果の式となります。
　　積分は微分の逆演算で原始関数に戻されます。
　　結果は積分定数Cを除いたものになります。

　［例］
     print intgr$("2*x+2")
     x^2+2*x
     print intgr$("x^2+5*x")
     (1/3)*x^3+(5/2)*x^2


 

DINT

　［機能］　定積分（数値）を求めます。

　［書式］　DINT(式の文字列,n1,n2)

　［説明］
　　 4
　　∫　f(x) dx　　（f(x)は式の文字列で例の場合だと 2*x+2）
　　 1
　　式f(x)を微分した原始関数F(x)のxにn1,n2を代入して F(n2)-F(n1) とした値が得られます。
　　式がx^2の時の定積分の結果はn1<=x<=n2 の範囲で
　　x軸と式の放物線の間で囲われた部分の面積となります。

　［例］
     print dint("2*x+2",1,4)
      21


 

FCAL

　［機能］　式どうしの計算をして結果の式を文字列で返します。

　［書式］　FCAL(式の文字列1,式の文字列2,"add"|"sub"|"mult")

　［説明］
　　xについての式（デフォルト）を計算します。
　　第三パラメーターで足し算"add"、引き算"sub"、掛け算"mult"を指定します。
　　計算できるのは係数が整数の式です。分数を含む式は現在未対応です。

　［例］
     print fcal("x+3","2*x+2","add")
     3*x+5
     print fcal("x^2+1","2x-2","mult")
     2*x^3-2*x^2+2*x-2

　係数と変数xの間の*（掛ける）の省略記述について。

　3x^2+4x+1　…①
　3*x^2+4*x+1　…②

　通常数学では①のような表記ですが
　Basicでは②のようにxの前に *（掛ける）を省略せずに記述して
　取り扱える式となります。
　関数に与える式は①と②両方使うことができますが（①は内部的に②に変換されて処理されます）
　関数が返す文字式は必ず②の書式で返されます。
　この②で返された文字式はxに数値を代入したあと
　そのままcalc("xの文字式")で計算して値を取得することができます。
　例
　　f$=fcal("x+3","2*x+2","add") :'2つの式が足されてf$に結果の3*x+5が入る
　　x=2 :'xに2を代入
　　print calc(f$) :'代入された値で3*x+5を計算
　　 11  :'結果の11が表示される

　また式の計算結果のxの係数は割り切れない無理数になることもあるので
　式の結果出力は小数でなく (1/3)*x^3+(5/2)*x^2 のように
　括弧で囲われた分数（割り算）で返されることになります。
　例　積分計算の場合
　　 print intgr$("x^2+5*x")
　　 (1/3)*x^3+(5/2)*x^2